行列や実数の諸性質も明らかにされていった。
5次方程式の非可解性や非ユークリッド幾何学の無矛盾性など
古来からの命題が否定的に解決されたことから数学の万能性に暗雲が立ち込めてきた。
アドリアン=マリ・ルジャンドル 素数定理の予想
\(x以下の素数の個数: \pi(x)は,\)
\(\pi(x) \sim \int_2^{x}\frac{dt}{\log{t}} \)
ルジャンドル記号
\( a, pが互いに素で, x^2 \equiv a\ (\mod \ p)\ が解を持つとき,\)
\( aはpを法として平方剰余であるといい,\)
\( (\frac{a}{p})=1 \)
\( 解を持たないとき, (\frac{a}{p})=-1 \)
\( (\frac{ab}{p})=(\frac{a}{p})(\frac{b}{p}) \)
ヤコビ記号 1837
\( 任意の整数aと任意の奇数nに対してnの素因数分解をn={p_1}^{\alpha_1}{p_2}^{\alpha_2}\cdots {p_k}^{\alpha_k}とすると, \)
\( (\frac{a}{n})=(\frac{a}{p_1})^{\alpha_1}(\frac{a}{p_2})^{\alpha_2}\cdots (\frac{a}{p_k})^{\alpha_k} \)
カール・フリードリヒ・ガウス
ガウス記号
\( [x]: xを超えない最大の整数 \)
\( [3]=3, [3.1]=3, [-3.1]=-4 \)
ガウス整数
実部と虚部がともに整数である複素数。
\( a+bi (a, b \in \mathbb{Z}) \)
最小二乗法 (ルジャンドルと先取権で争う)
正17角形の作図 1796
代数学の基本定理の証明
複素数係数のn次方程式は複素数の範囲で重複を許してちょうどn個存在する。
平方剰余の相互法則 1801
\( (\frac{2}{p})=(-1)^{\frac{p^2-1}{8}} \)
\( (\frac{p}{q})(\frac{q}{p})=(-1)^{\frac{p-1}{2}\frac{q-1}{2}} \)
ガウス積分
\( \displaystyle \int_{-\infty}^{\infty}e^{-ax^2}dx=\sqrt{\frac{\pi}{a}} \)
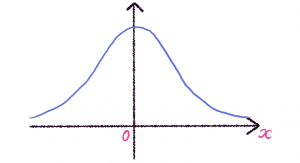
ガウス分布(正規分布)
確率密度関数が以下で表される分布。
\( \displaystyle f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \)
\( 平均は\mu, 分散は\sigma^2になる. \)
データ数が2の冪のときの高速フーリエ変換
ガウス=ルジャンドルのアルゴリズム
円周率を求める高速なアルゴリズム。
1回の反復で精度がほぼ倍になる。
2009年にはこのアルゴリズムを用いてコンピュータで2兆桁まで求められた。
\( \displaystyle a_0=1, b_0=\frac{1}{\sqrt{2}}, t_0=\frac{1}{4}, p_0=1 \)
\( \displaystyle a_{n+1}=\frac{a_n+b_n}{2} \)
\( \displaystyle b_{n+1}=\sqrt{a_n b_n} \)
\( \displaystyle t_{n+1}=tn-pn(an-a_{n+1})^2 \)
\( \displaystyle p_{n+1}=2p_n \)
\( で反復するとき, \)
\( \displaystyle \pi \simeq \frac{(a+b)^2}{4t} \)
フリードリヒ・ヴィルヘルム・ベッセル ベッセル関数
-
第一種ベッセル関数
-
第二種ベッセル関数
カスパー・ベッセル 複素数平面 1798
ジョージ・グリーン グリーンの定理
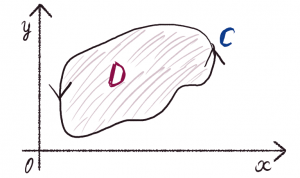
\( \displaystyle \oint_{C} Pdx+Qdy=\int\int_D(\frac{\partial Q}{\partial x} – \frac{\partial P}{\partial y})dxdy \)
オーギュスタン=ルイ・コーシー
コーシーの収束判定法
\( \displaystyle 正則級数\ \sum_ {n=1}^{\infty}a_n (a_n\geq 0) の収束性は, \)
\( L=\lim_{n \rightarrow \infty}\sqrt[n]{a_n} とするとき, \)
\( L<1のとき収束, L>1のとき発散, L=1のとき判定不能. \)
コーシー列
\(数列a_nがコーシー列であるとは, 任意の正の数\epsilonに対してある自然数Nが存在して,\)
\(m, n>N\Rightarrow |a_n-a_m|<\epsilon が成り立つことである. \)
\(数列が収束することとコーシー列であることは同値である.\)
コーシーの平均値の定理 1823
\(閉区間[a, b]において連続, 開区間(a,b)において微分可能な関数f(x), g(x)に対して, g(b)-g(a)\neq 0ならば,\)
\( \displaystyle \frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(c)}{g'(c)} \)
\( を満たすc (a<c<b)が存在する. ただしg'(c)\neq 0 \)
コーシー・リーマンの関係式 複素関数が微分可能か
\( 領域D内の任意の点z=x+yiに対して複素関数f(z)を, \)
\( f(z)=f(x+yi)=u(x, y)+v(x, y)i とする. \)
\( \displaystyle \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x} \)
\( を満たすとき正則であるという. \)
コーシーの積分定理
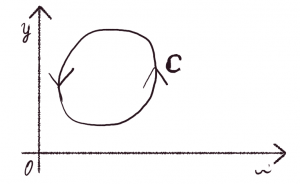
正則な領域を囲む単純閉曲線の周回積分は0になる.
\( \displaystyle \oint_{C} f(z)dz=0 \)
留数定理
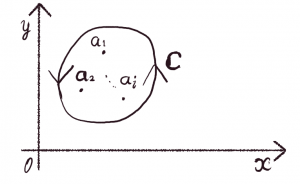
\( \displaystyle Res(a)=\frac{1}{(n-1)!}\lim_{z \rightarrow a} \frac{d^{n-1}}{dz^{n-1}}\{(z-a)^nf(z)\} \)
\( 閉領域Cの孤立特異点をa_1,a_2,\cdots , a_i とするとき, \)
\( \displaystyle \oint_{C} f(z)dz=2\pi i \sum_{k=1}^i Res(a_k) \)
実対称行列の固有値が全て実数 1829
ジョゼフ・フーリエ
フーリエ級数
\( \displaystyle f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos{nx}+b_n\sin{nx}) \)
\( \displaystyle a_n=\frac{1}{\pi}\int_{-\pi}{\pi}f(x)\cos{nx}dx \)
\( \displaystyle b_n=\frac{1}{\pi}\int_{-\pi}{\pi}f(x)\sin{nx}dx \)
フーリエ変換
\( \displaystyle f(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{-i\omega t}d\omega \)
フーリエの法則、熱伝導方程式
\( \displaystyle J=-\lambda \frac{\partial T}{\partial x} \)
フォイエルバッハの定理 1822
- 三角形の三辺の中点、三つの垂線の足、垂心と三頂点の中点の九点は同一円上にある。
- 九点円は内接円と内接し、三つの傍接円に外接する。
ニールス・アーベル
5次方程式の非可解性 1824
楕円曲線上のアーベル群
エヴァリスト・ガロア ガロア理論 1830頃
群・環・体
整数や有理数上での演算を一般化したい。
群は集合と二項演算で定義され、演算後も群の集合に入る。単位元が存在し、任意の元に逆元が存在するものをいう。
環は群に2つめの二項演算を導入し、1つめの演算に対して可換であり、結合法則と分配法則が成り立つものをいう。
体は環であり2つめの二項演算に対して0以外に逆元が存在するものをいう。
\(\{\mathbb{Z}, +\}は群. \{\mathbb{Z}, +, *\}は環. \{\mathbb{Q}, +, *\}は体である. \)
群(環・体)の要素数を位数といい、位数が有限のものを有限群(環・体)という.
群の部分集合がまた群になっているとき部分群という.
アーベル群(可換群)
群の任意の元に対する演算が交換法則を満たすもの。
正方行列と行列の積の演算はアーベル群でない。
ガロア体(有限体)
\( 有限体の位数は素数のべきである必要があり, GF(p^k) で表す. \)
\( 有限体は必ず可換になり, 位数が同じ有限体は同型である. \)
巡回群
\( g \in Gによって生成される部分群H=<g> \)
\(\{ e,g,g^2,g^3,\cdots,g^{n-1} \}\)
\( 有限群の場合はg^n=eとなるnが存在する. \)
剰余類
\(群Gと部分群H, g \in G \)
\( gH={gh: h \in H}\ : 左剰余類\)
\( Hg={hg: h \in H}\ : 右剰余類\)
gH=HgのときHを正規部分群という. (可換なら常に一致する)
商群
\( 群Gとその正規部分群Hに対して, (G/H=\{H, Ha_1, Ha_2,\cdots\}は群となる.\)
\( \mathbb{Z}/n\mathbb{Z}は位数nの巡回群である. \)
対称群
\( (1,2,\cdots,n)を並べ替える操作(置換)の集合は群になり, 対称群:S_n という. \)
\(n個のうち2つだけを入れ替える置換を互換という.\)
\(任意の置換は互換の積で書け, 置換によって互換の積の個数が偶数か奇数かが決まっている.\)
交代群
\( S_nのうち偶置換のみを取り出すと群になり, 交代群: A_nという.\)
\( n\leq3でA_nはアーベル群. n\geq4でA_nは非可換群.\)
\( A_nはS_nの正規部分群である. \)
\( A_4はクラインの4元群:V_4を正規部分群にもつ. \)
\( n\geq5でA_nは正規部分群を自明な\{e, A_n\}しか持たない単純群である. \)
代数方程式の可解条件を決定
\(n次方程式のガロア群がS_nに等しい.\)
\( S_n=G_0\triangleleft G_1\triangleleft\cdots \triangleleft G_m となる正規部分群列で,\)
\( G_m=\{e\}, G_{j-1}/G_{j}が巡回群となるものが存在する. \)
\( 五次方程式ではS_5\triangleleft A_5\triangleleft eの列しかありえないが, \)
\( A_5/e=A_5が巡回群 \Rightarrow A_5はアーベル群となるが矛盾する. \)
\( よって五次方程式は可解でない. \)
ジョージ・ブール ブール代数
\(0と1だけの要素からなる代数。後のノイマン型コンピュータでのビット演算に対応する. \)
\( x \land y: x=y=1のときのみ1. \)
\( x \lor y: x=y=0のときのみ0. \)
\( \lnot x: x=1のとき0, 0のとき1. \)
ペーター・グスタフ・ディリクレ
鳩の巣原理 1834
ディリクレのディオファントス近似定理
\( \displaystyle |\alpha-\frac{p}{q}|<\frac{1}{qN}を満たすものが存在する. \)
非ユークリッド幾何学
ボヤイ・ヤーノシュ
平行線公準を満たす幾何学と満たさない幾何学のどちらが正しいのかは決定できない。
ニコライ・イワノビッチ・ロバチェフスキー
平行線論の幾何学的研究 1840
双曲幾何学を導く
シメオン・ドニ・ポアソン ポアソン分布
\(P(X=k)=\frac{\lambda^k e^{-\lambda}}{k!}\)
カール・グスタフ・ヤコブ・ヤコビ ヤコビ行列(ヤコビアン)
\( \displaystyle x_1=g_1(y_1,y_2,\cdots,y_n), x_2=g_2(y_1,y_2,\cdots,y_n), \cdots, \)
\( \displaystyle x_n=g_n(y_1,y_2,\cdots,y_n)によってg(y_1,y_2,\cdots ,y_n)に変数変換するとする. \)
\( このとき \)
\( \int\!\!\!\int\!\!\cdots\!\!\int f(x_1,x_2,\cdots ,x_n)dx_1dx_2\cdots dx_n=\int\!\!\!\int\!\!\cdots\!\!\int g(y_1,y_2,\cdots ,y_n)|J|dy_1dy_2\cdots dy_n \)
\(Jはヤコビ行列 \)
J = \left(
\begin{array}{cccc}
\frac{\partial x_1}{\partial y_1} & \frac{\partial x_1}{\partial y_2} & \ldots & \frac{\partial x_1}{\partial y_n} \\
\frac{\partial x_2}{\partial y_1} & \frac{\partial x_2}{\partial y_2} & \ldots & \frac{\partial x_2}{\partial y_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial x_n}{\partial y_1} & \frac{\partial x_n}{\partial y_2} & \ldots & \frac{\partial x_n}{\partial y_n}
\end{array}
\right)
\)
ヤコビの楕円関数
\( u=\int_0^{\phi}\frac{d\theta}{\sqrt{1-m\sin^2{\theta}}} \)
\( sn\ u=\sin{\phi} \)
\( cn\ u=\cos{\phi} \)
二重周期性を持つ解析関数。三角関数のような加法定理が成り立つ。
オーガスタス・ド・モルガン ド・モルガンの法則
\( \lnot(P \land Q)=\lnot P \lor \lnot Q \)
シャルル・エルミート
エルミート内積
\( n次複素ベクトル \textbf{u,v}に対して, \)
\( <\textbf{u,v}>=x_1\overline{y_1}+x_2\overline{y_2}+\cdots +x_n\overline{y_n} \)
\( をエルミート内積という. \)
エルミート行列
正方行列が転置して複素共役をとったときに元の行列と等しいときエルミート行列であるという.
- 固有値が実数
- 異なる固有値の固有ベクトルが直交
- ユニタリー行列で対角化可能
エルミート多項式
\( \displaystyle (\frac{d^2}{dx^2}-2x\frac{d}{dx} +2n)H_n(x)=0 \)
\( を満たす多項式\ H_n(x)\)
エルミート作用素
ウィリアム・ローワン・ハミルトン
ハミルトン路
ハミルトン路を求める問題はNP完全である。
四元数 1843
\(3つの虚数i, j, kを用いてw+xi+yj+zkと表される数.\)
\(乗法の交換法則は成り立たない非可換体である。 ij=-ji=k\)
三次元空間の回転
四元数はハミルトンが推して電磁気学にも応用しようとしたが普及しなかった。
現代では三次元空間での回転が他の方式より優れていることから
コンピュータグラフィックや姿勢制御などで使われている。
ケイリー・ハミルトンの定理 1858
\( 正方行列Aに対して, f(\lambda)=det(A-\lambda I )とする. \)
\( f(A)=O である. \)
フェルディナント・アイゼンシュタイン アイゼンシュタイン整数 1844
\( a+b\omegaの形の複素数. \)
ジョゼフ・リウヴィル
リウヴィルの定理(代数) 1844
リウヴィル数: 超越数であることが証明された初めての数 1844
\( xが有理数体上次数nの代数的無理数であれば、ある定数 c(x) > 0 が存在して,\)
\(任意の整数 p と q, ただし q > 0, に対し,\)
\( |x-\frac{p}{q}|>\frac{c(x)}{q^n} \ が成り立つ. \)
\( \displaystyle l=\sum_{k=1}^{\infty} 10^{-k!} \ 上記の式を満たさないので超越数である. \)