座標に依らない一般的な法則を導き出そうとする動きが解析力学を生んだ。
それらを数学的な裏付けを持って進めたのが天才オイラーである。
化学反応を伴う実験によって多くの元素の性質を見出した。
科学的な進展は電池の発明を待つこととなる。
カール・フォン・リンネ 動植物の分類法 1735
- ラテン語を用い、属と種の名を列記する二名法を発明
- 植物の階層分類体系を創設
ダニエル・ベルヌーイ サンクトペテルブルグのパラドックス 1738
\( このゲームの参加費はいくらが適当か。\)
とても無限大の参加費が適当とは思えないパラドックス。
小さな確率と大きな値に対しての期待値で論じても意味のないことが多い。
ベルヌーイの定理(流体力学)
\( \frac{1}{2}\rho v^2 + p + \rho gh = C \)
\( v: 流速、rho: 密度、P: 圧力、g: 重力加速度、h: 基準面からの高さ、C: 定数\)
レオンハルト・オイラー 1707-1783
オイラーの公式
\( \displaystyle e^{i\pi}+1=0 \)
ゴールドバッハ予想 1742
非常に大きな数まで成り立っていることがコンピューターで調べられているが、
証明はされていない。
オイラー路:ケーニヒスベルクの橋 1753
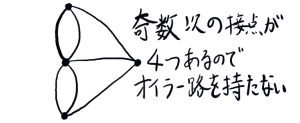
グラフの全ての辺を通る路のこと。また全ての辺をちょうど1度だけ通る閉路は、オイラー閉路と呼ぶ。
連結グラフにおいて、
オイラー閉路はすべての頂点の次数が偶数と同値
オイラー路は奇数次の頂点の個数が2個まで
オイラーのφ関数 1760
\( n={p_1}^{k_1}{p_2}^{k_2}\cdots {p_r}^{k_r}と素因数分解されるとき,\)
\( \phi(n)= n(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots (1-\frac{1}{p_r})\)
\( a^{\phi(n)} \equiv 1 (\rm{mod}\ n) \ \ ただしaとnは互いに素 \)
オイラー線
三角形の重心G、外心O、垂心Hは同一直線上にあり、この直線をオイラー線という。
また、重心GはOHを1:2に内分する。
ベータ関数・ガンマ関数
\( \displaystyle B(p, q) = \int_0^1 x^{p-1}(1-x)^{q-1}dx \)
ジャン・ル・ロン・ダランベール ダランベールの収束判定法
\( \displaystyle \lim_{n \rightarrow \infty}\frac{a_{n+1}}{a_n} < 1 のとき絶対収束する.\)
\( \displaystyle \lim_{n \rightarrow \infty}\frac{a_{n+1}}{a_n} > 1 のとき発散する.\)
\( \displaystyle \lim_{n \rightarrow \infty}\frac{a_{n+1}}{a_n} = 1 のときどちらともいえない.\)
クラメルの公式 1750頃
\( \displaystyle x_i = \frac{|\boldsymbol{A}_i|}{|\boldsymbol{A}|} \)
\( \boldsymbol{A}_iは行列\boldsymbol{A}のi列目をベクトル\boldsymbol{B}のi番目の要素に変えたもの. \)
ライデン瓶 1746
ガラス瓶に金属箔を二重に貼り付けたもの。
コンデンサーの原理で電荷を蓄えることができる。
検電器 1750
ベンジャミン・フランクリン 電気、避雷針
凧糸で落雷をライデン瓶に蓄え、雷が電気であることを証明 1752
避雷針の設置 1760
ノレ 浸透圧の発見 1748
ベイズ ベイズの定理 1763
\( 事象Bが起こるという条件のもとで事象Aが起こる条件付き確率P(A|B)は, \)
\( P(A|B)=\frac{P(B|A)P(A)}{P(B)} \)
ジョゼフ=ルイ・ラグランジュ 解析力学 1788
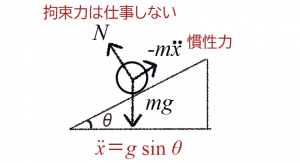
ダランベールの原理
動力学を静力学(釣り合い)として帰着できる。
ラグランジュの未定乗数法
\( f(x_1,x_2,\cdots ,x_n)がg(x_1,x_2,\cdots ,x_n)=0の条件下で最大化する問題を考える. \)
\( L(x_1,x_2,\cdots ,x_n,\lambda)=f(x_1,x_2,\cdots ,x_n)-\lambda g(x_1,x_2,\cdots ,x_n)として, \)
\( \displaystyle \frac{\partial L}{\partial x_1}=\frac{\partial L}{\partial x_2}= \cdots = \frac{\partial L}{\partial x_n} = \frac{\partial L}{\partial \lambda} = 0 を満たす. \)
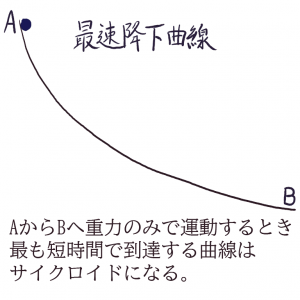
最小作用の原理
運動は作用と呼ばれる汎関数を最小にするような軌道に沿って実現される。
神様が謎の量:作用を最小化するように世界は作られているという考え方だが、
実際屈折の法則や最速降下曲線が説明できたことから物理学の根底原理として信仰されている。
汎関数と変分法
あらゆる関数の中から最小作用の原理を満たす関数を見つけるために変分法を使う.
\( x, y(x), y'(x)の積分形からなる関数Iを汎関数という. \)
\( \displaystyle I=\int_{x_1}^{x_2}f(x, y, y’) dx の極値は, \)
\( \displaystyle \frac{d}{dx}\frac{\partial f}{\partial y’}-\frac{\partial f}{\partial y}=0 \)
オイラー・ラグランジュ形式の運動方程式
\( T:運動エネルギー, U:ポテンシャルエネルギーとして,\)
\( ラグランジアンLをL=T-Uとおく. \)
\( \displaystyle \frac{d}{dt}\frac{\partial L}{\partial \dot{x}} – \frac{\partial L}{\partial x}=0 \)
座標変換に対してこの式は不変である。
ハミルトン形式:ルジャンドル変換
\( ラグランジアンL(q, \dot{q})に対して, \)
\( \displaystyle 一般化運動量: p=\frac{\partial L}{\partial \dot{q}} を定義する.\)
\( \displaystyle ハミルトニアン: H=pq-Lは, \dot{p} = \frac{\partial H}{\partial q}, \dot{q} = -\frac{\partial H}{\partial p}.\)
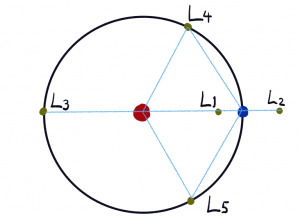
ラグランジュ点 1772
恒星・惑星系において質量が無視できるぐらい小さな天体が釣り合うポイント。
\( L_4, L_5 \) は釣り合いの位置からずれても位置を保とうとする安定な軌道となる。
ピエール=シモン・ラプラス
ラプラス変換 1780
時間tの関数から複素数sの関数に変換する積分。
$$ F(s) = \int_{0}^{\infty}f(t)e^{-st}dt $$
微分方程式をラプラス変換してsの代数方程式として解いた後、
逆ラプラス変換して元の微分方程式の解を求めることができる。
ラプラスの悪魔 1812
ある瞬間における全ての物質の力学的状態と力を知ることができ、
それを解析することができたならば、未来を完全に予測することができるだろう。
メートル法
科学はもとより商売においても使いにくい。
統一的な単位を制定しようとする動き。
測量によって1メートルを定めた。
この定義はラプラスが提案した。
ここで定めた1メートルに対して0.1m立法の体積を1リットル。
1リットルの水の質量を1キログラム。
10メートル平方の面積を1アールと定めた。
シャルル・メシエ メシエ天体カタログ
シャルル・メシエが作成した星雲・星団・銀河のカタログ。
平賀源内のエレキテル 1776
摩擦を利用した静電気の発生装置と蓄電池がセットになっている。
溜めた静電気を放出させて観客を驚かせた。
ジェームズ・ワット 蒸気機関の改良 1776頃
ジョン・ハリソン 航海で経度を測定するに足りる精度の時計
1730~1770頃に順次精度を上げた時計を製作。
最終的に1日あたり1秒以下の誤差を達成した。
火の素は何か?
フロギストン説
古代ギリシャの頃から「火」は五大元素の一つと数えられ、燃焼に関わる元素と考えられてきた。
化学の黎明期では可燃性の物体にはフロギストンが含まれているとされた。
物を燃焼させると、物質からフロギストンが放出されて灰が残るという考えだ。
このフロギストン説は「気体の性質」や「化学反応の質量変化」に着目した実験によって否定されていく。
ジョゼフ・ブラック 固定空気(二酸化炭素)の発見 1754
気体という概念が存在せず。空気以外の気体など想像もしなかった時代。
ブラックは石灰石(炭酸カルシウム)を強熱すると、空気とは異なる気体が生成することを発見した。
石灰水を白濁させ、火を消してしまう気体を固定空気と呼んだ。
ヘンリー・キャヴェンディッシュ 水素の発見 1766
金属に強酸を加えると可燃性の気体が放出される。
この気体は非常に軽いのでフロギストンではないかという仮説を立てた。
アントワーヌ・ラヴォアジエらによるフロギストン説の否定
- リンや硫黄を空気中で燃やすと質量が増える ラヴォアジエ 1772
- 密閉された容器内に金属を入れて燃焼させると燃焼後の質量は燃焼前と変わらないが、
その後容器に穴をあけると、空気が容器内に音を立てて流れ込み、質量が増える。 ラヴォアジエ 1774- これらの事実から燃焼とは空気中の何かを吸収して重くなる現象であるとラヴォアジエは考えた。
- 酸化水銀を強熱したときに発生する気体は固定空気とは違う カール・ヴィルヘルム・シェーレ 1773
- この気体にはろうそくが激しく燃えたり、
動物を気体で満たした瓶に閉じ込めておくと空気の瓶より長生きする性質があった。
- この気体にはろうそくが激しく燃えたり、
- 動物の呼吸で燃焼と同じ固定空気が生成される ラヴォアジエ 1777
- 動物の呼吸と燃焼は等しい原理なのではないかと考えた。
- 空気が呼吸できるもの1/4、呼吸できないもの3/4からなることを発表 ラヴォアジエ 1778
- 今でいうところの窒素と酸素である。
- 空気のうち、呼吸ができる方は燃焼を助ける働きがあり、酸の素ではないかと考え酸素と命名 ラヴォアジエ 1779
- 植物の緑色の部分が固定空気を浄化する。光合成の発見。 ヤン・インゲンホウス 1779
- ラヴォアジエは固定空気が酸素に変わっていることを確認。
- フロギストンと思われていた気体を燃焼させると水ができる。 プリーストリーとキャヴェンディッシュ 1781
- フロギストン説で説明しようとした。
- 質量保存の法則 ラヴォアジエ 1782
- 「化学反応の前と後で物質の総質量は変化しない」
- プリーストリーらの実験を追試し、水素と名付ける ラヴォアジエ 1783
フロギストン説だと負の質量やら、脱フロギストンの反応などを仮定しないと説明できない。
ラヴォアジエはフロギストンを仮定しない方がこの結果を簡単に説明できるとした。
織物の漂白に塩素が用いられる 1783
熱気球 1783
シャルル・ド・クーロン クーロンの法則 1785
荷電粒子間に働く力は、電荷量の二乗に比例し、距離の二乗に反比例する。
\( F=\frac{1}{4\pi \epsilon}\frac{q_1 q_2}{r^2} \)
\( \epsilonは真空の誘電率 \)
ジャック・シャルル ボイル=シャルルの法則
$$ PV=nRT $$
気体の圧力と体積の積は温度と物質量に比例する。
この性質が成り立つ気体を理想気体という。
比例定数\(R\)を気体定数という。
アペール 瓶詰め・缶詰 1795
フランス政府による食品の長期保存方法の公募で採用。
調理済みの食品をビンに詰め、コルク栓で密封した後に煮沸消毒を行うことで長期保存可能となる。
- ブリキの缶詰 1810
- 缶切りの発明 1858
ウィリアム・ハーシェル
星雲のカタログ 1786
後にNGCカタログとなりまとめられる。
天王星の発見 1781
天王星とされる天体は過去にも観測されていたが、誰も惑星だとは考えなかった。
軌道計算を行ったところ、恒星や彗星ではなく惑星であることが明らかになった。
ウランの発見 1789
同時期に発見された天王星の名前にちなんで名付けられる。
蛍光性を持ち、ガラスなどに使われた。 (ウランガラス)
赤外線の発見 1800
プリズムで太陽光を分光したときに、赤の外側の領域には物を温める見えない光が存在している。
ヘンリー・キャヴェンディッシュ 万有引力定数の計測 1798
キャベンディッシュは「ねじり天秤」を用いて万有引力定数と地球の質量を測定した。
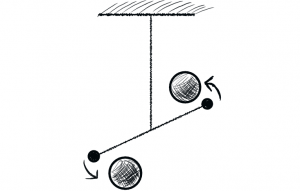
小球に働く万有引力は非常に小さいが、
それを周期という比較的長い時間で測定することで精度が出る。
チャールズ・テナント さらし粉の発明 1799
\( {\rm Ca(OH)2} + {\rm Cl_2} \longrightarrow {\rm CaCl(ClO)\cdot H_2O} \)
より安全に塩素を使った漂白を扱えるようになる。